Introduction to the principle of the integrating sphere|Working principle of the integrating sphere

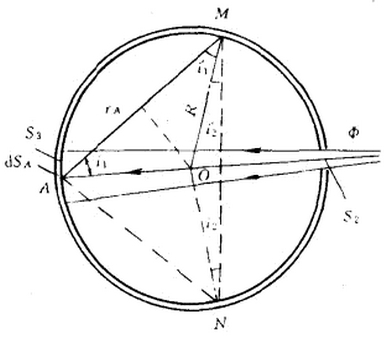
It is assumed that the total luminous flux of a beam entering the integrating sphere is Φ, and the area of ​​the inner wall of the bulb is S3. Light diffuses multiple times on the inner wall surface. Now look at the illuminance E at any point M on the inner wall. Since the light entering the integrating sphere directly shines at S3, a part of the light diffused and reflected by each point on S3 will be directly at the inspection position M, and the sum of the illuminances of all the light directly incident at M is called direct illumination. Expressed by E0. In addition, there is light diffused from S3 to the inner wall of the integrating sphere through multiple diffuse reflections to reach M. The sum of the illuminances is called multiple diffuse illuminance, which is represented by E∑. Therefore, the illuminance E at the position M is examined as the sum of the illuminances of the two parts, namely: E=E0+E∑ (1-1)

Direct illumination E0

The small surface element dSA is taken at any point A in the range of S3, and the total luminous flux incident on the surface element is dΦ, then the illuminance EA at the position A is: EA=dΦ/dSA, and the inner wall of the integrating sphere can be regarded as an ideal diffuse. The reflector, so the luminance LA at A is: LA = EAρ / π (where ρ is the diffuse reflection coefficient). If a small bin dSM is taken at the location M, the luminous flux from the bin dSA with the luminance LA to the dSM bin is: dΦA=LAdSAcosi1dSMcosi1'/rA2

The physical quantities in the formula are shown in the figure. It can also be seen from the figure that i1=i1', rA=2Rcosi1 (R is the radius of the inner wall of the integrating sphere). The illuminance formed by the light emitted by the bin dSA at the inspection position M: dE0=dΦA/dSM=LAdSAcosi1cosi1'/rA2=LAdSA/4R2www.LisunGroup.com.cn

After the physical quantities in the formula are fed and collated, the direct illuminance of the entire S3 diffuse reflection light at M is obtained: E0=ρ∫S3dΦ/4πR2=ρΦ/4πR2 (1-2)

Where Φ is the total luminous flux entering the integrating sphere.

Multiple diffuse illuminance E∑

Now, if any position N on the inner wall is obtained, the direct light from S3 is obtained, and then the light is again diffused and directly reaches the light at the inspection position M. This portion is called an additional illuminance E1. www.LisunGroup.com.cn

Since the direct illuminance E0 is also obtained at N, the luminance L0 is L0 = ρE0 / π. The face element dSN is taken at N, and an additional illuminance dE1 formed at the position M from the dSN is expressed as: dE1=dΦ1/dSN=L0dSNcosi2dSMcosi2'/4R2cosi2cosi2' dSM=L0dSN/4R2

The total primary illuminance E1 formed at the position M is diffusely reflected by the inner wall of the integrating sphere: E1=ρE0∫SdSN/4πR2=ρE0S/4πR2=ρE0(1-f)S1/4πR

Where S1 is the area of ​​the inner wall of the entire ball; f is the opening ratio (f=S2/S1, and S2 is the spherical area at the opening).

Substituting S1=4πR2 into the above formula: E1=ρ(1-f)E0 (1-3)

According to the same method, the secondary illuminance E2 formed by M at one position of the illuminance at the inner wall, the three illuminances E3, and the like can be derived:

E2=ρ(1-f)E1=[ρ(1-f)]2E0

E3=ρ(1-f)E2=[ρ(1-f)]3E0www.LisunGroup.com.cn

Thus, the total illuminance E∑ of multiple diffuse reflections is: E∑=E1+E2+E3+...=E0ρ(1-f)/[1-ρ(1-f)] (1-4)

Thus, the total illuminance E at the position M is examined: E = E0 + E ∑ = E0 / [1 - ρ (1-f)] (1-5)

Feeding the above formula (1-2), we get: E=ρΦ/4πR2[1-ρ(1-f)] (1-6)

It can be seen from the above formula that the illuminance at any position on the inner wall is proportional to the total luminous flux entering the integrating sphere. This is the basic formula for applying the integrating sphere to measure the luminous flux of the source.

Hongzhan has a research institute specializing in the research and development of environmental test equipment. It has mature loop test development methods and laboratories, and gathers a group of outstanding talents and well-known experts in the industry. The strong R&D team leads the domestic loop test technology. Development direction. At present, the company has high and low temperature test chambers with independent intellectual property rights, high and low temperature wet heat test chambers, rapid temperature change test chambers, thermal shock test chambers, three comprehensive test chambers, high and low temperature low pressure test chambers, solar radiation test chambers. The climatic environment test equipment and customized products such as industrial ovens and walk-in high and low temperature damp heat test chambers and high wind speed rain test chambers are at the leading domestic level and international high standards.

Stacking Chairs

For a truly unique style, try our stackable ghost chairs that are also ideal for making a small space look larger. Stacking stools can complete the bar at any event or restaurant, while our outdoor selection can complete any patio or outdoor venue space. No matter what kind of audience you`re designing for, our chairs can help you achieve your vision.

Stacking Chairs,Stackable Chairs,Stackable Dining Chairs,Stacking Patio Chairs

jiangsu concentric internatinal ltd , https://www.jsconcentriccorp.com